This is the third of three posts on how the Massachusetts special election interacts with health care reform:

After a lot of feedback and hard thinking, I conclude that this is extremely difficult to predict. Here are the subjective judgments I’m making:

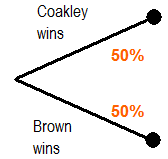
  • I assume the Massachusetts race is a toss-up.
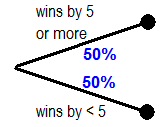
  • I assume there is a difference in the impact on health care legislation of a slim Coakley win and a big Coakley win. I am setting the breakpoint at +5.
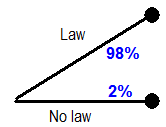
  • I assume a 98/2 chance of legislative success (signed law) if Coakley wins big, and a 90/10 chance if she wins by a slim margin.
  • If Brown wins:
    • I’ve got collapse at 45%.
    • I assume reconciliation and a deal with Senator Snowe are super-long shots. Reconciliation is hard and extremely unsatisfying to the bill’s advocates, and a deal with Snowe is probably too far gone.
    • That leaves “ram it through” and “House folds.” I keep bouncing between 2:1 in each direction. So I ended up saying equal chances for each.

Before Tuesday’s election, I predict a 75% chance that there will be a health care law. If Brown wins, I predict a 55% chance of a law and a 45% chance that legislation implodes, with the most likely scenarios being ram it through the Senate before Brown is seated, and the House folding and passing the Senate bill.

Build your own health care legislation decision tree

If you care a lot about this and think my subjective judgments are crazy, then I will help you build your own decision tree. This is called Bayesian analysis. It sounds difficult but it’s not. I will walk you through it, step by step.

You can click on any diagram for a larger view.

Step 1: What is your projection for the Massachusetts Senate race? You can use polling data, expert analysis, or look at what the market is predicting. I played it safe and called the race a toss-up.

Step 2: I think there’s a difference in the legislative impact of a big Coakley win and a narrow Coakley win. I set the breakpoint at +5. Choose your own breakpoint and set probabilities. Assuming Ms. Coakley wins, what is the chance of a big win vs. a narrow win? I have no idea, so I again chose a 50/50 split.

Step 3: Assume Ms. Coakley wins big. What is the chance of a signed law? Everyone seems to think it’s quite high, but is that 90%, 95%, 98%, 100%? I’m guessing 98/2.

Step 4: Assume Ms. Coakley wins a narrow victory. What is the chance of a signed law? It’s lower than under a narrow victory, but how much lower? Leader Reid still has 60 votes, but do nervous Democratic Members bolt because they’re scared of losing reelection? I think a narrow Coakley victory has a fairly big effect, so I drop 98/2 to 90/10.

Step 5: This is the hard one. Assume a Brown victory. What path do the Democratic leaders choose, and how likely is collapse? You can review my analysis and the procedural options. The probabilities you assign to these five branches must add up to 100%. Here are my predictions.

Step 6: Put them all together. Multiply the probabilities as you move down each branch of the tree and write the results at the end of each branch. As an example, the “Ram it through” leg on my chart has a 50% X 25% = 12.5% chance of resulting in a law. The “Coakley narrow margin and Democrats bolt” scenario has a 50% X 50% X 10% = 2.5% chance of resulting in no law.

Color results that end in a law in green, and those that do not in red. The result probabilities should add up to 100%. (Click the diagram for a larger view.)

Step 7: Calculate your pre-election probability of a law by adding up all the green results, and your pre-election probability of no law by adding up the red results. Here are my results:

  • Law = 74.5%
  • No law = 25.5%

I rounded this to get my 75% pre-election prediction of a law.

Step 8: You already know your “Coakley big win” and “Coakley narrow win” probabilities from steps 3 & 4. Calculate your “Brown victory scenario” probabilities like this:

  • Law if Brown wins = Add the blue probabilities for the first four scenarios under the Brown wins branch.
  • No law if Brown wins = Take the “collapse” probability under the Brown wins branch.

My results if Brown wins are:

  • Law = 55%
  • No law = 45%

Ta da!

Thanks for playing.